그래프
그래프의 개념
그래프는 노드(vertex)와 간선(edge)를 이용한 비선형 데이터 구조입니다. 보통 그래프는 데이터 간의 관계를 표현하는 데 사용합니다. 데이터를 노드로, 노드 간의 관계나 흐름을 간선으로 표현합니다.
간선에는 방향이 있을 수도 없을 수도 있고 관계나 흐름을 정의할 필요가 있다면 가중치라는 개념을 추가하여 표현합니다.
그래프 용어 정리
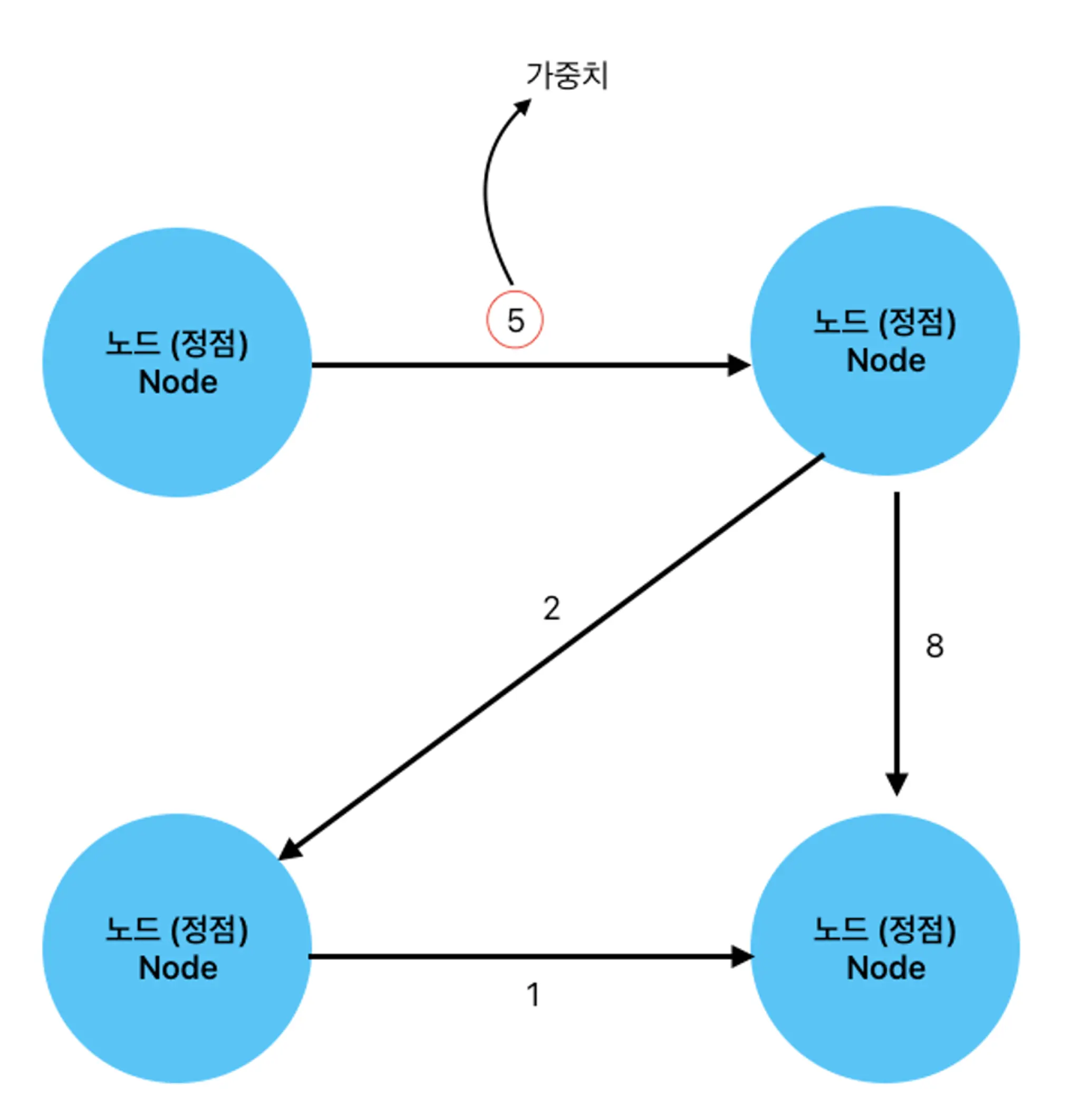
동그라미로 표현된 것이 노드, 화살표로 표현한 것이 간선, 간선 위에 숫자로 표현한 것이 가중치입니다.
그래프의 특징과 종류
그래프는 방향성, 가중치, 순환 특성에 따라 구분됩니다.
흐름을 표현하는 방향성
간선은 방향을 가질 수도, 없을 수도 있습니다. 방향이 있는 간선을 포함하면 방향 그래프, 방향이 없는 간선을 포함하면 무방향 그래프라고 합니다.
이때 방향 그래프는 한쪽만 가리키는 것이 아닌 서로 반대를 가리키는 간선이 있을 수도 있습니다.
흐름의 정도를 표현하는 가중치
두 번째 특성은 가중치입니다. 가중치는 흐름의 방향 뿐만 아니라 양도 중요할 수 있습니다. 이런 가중치가 있는 그래프를 가중치 그래프(weighted graph)라고 합니다.
시작과 끝의 연결 여부를 보는 순환
순환이 존재하는 그래프를 순환 그래프라고 하고, 순환이 존재하지 않는 그래프를 비순환 그래프라고 합니다.
그래프 구현
그래프의 구현 방식에는 인접 행렬과 인접 리스트가 있습니다.
인접 행렬 그래프 표현
2차원 배열을 활용하여 구현하는 경우가 많습니다. 이때 배열의 인덱스는 노드, 배열의 값은 노드의 가중치로 생각하고, 인덱스의 세로 방향을 출발 노드, 가로 방향을 도착 노드로 생각하면 자연스럽게 노드로 표현할 수 있습니다.
0 | 1 | |
|---|---|---|
0 | - | 400 |
1 | - | - |
인접 리스트 그래프 표현
인접 리스트 그래프 표현 방식은 다음과 같은 과정으로 동작합니다.
우선은 노드 개수만큼 배열을 준비합니다.
배열의 인덱스는 각 시작 노드를 의미하며 배열의 값에는 다음 노드를 연결합니다.
인접 행렬과 인접 리스트의 장단점
두 방식으로 그래프를 표현할 때 어느 한쪽이 매우 뛰어나거나 하지 않습니다. 모두 장단점이 있습니다.
인접 행렬의 장단점
인접 행렬은 크게 두 가지의 단점이 있습니다. 인접 행렬로 희소 그래프를 표현하는 경우 인접 행렬은 크기가 고정되어 최악의 경우를 고려해서 크기를 결정해야 합니다. 따라서 노드가 N개 있을 때 N x N 크기의 인접 행렬이 필요합니다.
인접 행렬의 장점은 간선의 정보를 확인할 때의 시간 복잡도가
인접 리스트의 장단점 인접 리스트는 인접 행렬과 정반대의 장단점을 가집니다. 인접 리스트는 실제 연결된 노드에 대해서만 노드의 값을 담아 연결하기만 하면 됩니다. 때문에 모든 노드가 연결되어 있을 경우 효율이 떨어질 수 있습니다. 하지만 그런 경우는 굉장히 드뭅니다. 보통은 인접 리스트를 활용하면 메모리를 아낄 수 있습니다. 특정 노드를 검색할 때 탐색 시간이
메모리 사용 | 시간 복잡도 | 기타 | |
|---|---|---|---|
인접 행렬 | 구현이 상대적으로 쉬움 | ||
인접 리스트 | M은 간선의 개수 |
그래프 탐색
그래프에서 탐색을 하는 방법은 2가지가 있습니다.
더 이상 탐색할 노드가 없을 때까지 방문, 더이상 탐색할 노드가 없다면 이전으로 되돌아가 방문하지 않은 노드를 방문(깊이 우선 탐색)
가까운 모든 노드를 방문 이후 가까운 모든 노드를 방문(너비 우선 탐색)
깊이 우선 탐색
깊이 우선 탐색은 시작 노드부터 탐색을 하여 최대 깊이까지 차례대로 방문합니다.
탐색을 시작하려면 시작 노드를 정하고, 스택에 시작 노드를 넣습니다. 스택에 있는 노드는 방문하지 않았지만 방문할 예정인 노드입니다.
다음을 고려해야합니다.
스택이 비었는지 확인해야 합니다. 스택이 비어있다면 모든 탐색이 마무리가 되었음을 알려줍니다. 스택이 없다면 종료합니다.
스택에서 노드를 팝합니다.
팝한 노드의 방문 여부를 확인합니다. 방문한 적이 없다면 방문 처리합니다.
방문한 노드와 인접한 모든 노드를 확인합니다. 그 중에서 방문하지 않은 노드를 스택에 푸시합니다. 스택은 LIFO 구조이므로 방문 순서를 오름차순으로 고려한다면 역순으로 푸시해야합니다.
탐색하는 과정에서 역방향으로 되돌아가는 동작을 백트래킹이라고 합니다. 스택은 최근 푸시한 노드를 팝할 수 있으므로 특정 노드를 방문하기 전에 최근 방문 노드를 팝 연산으로 쉽게 확인할 수 있습니다.
너비 우선 탐색
시작 노드와 거리가 가장 가까운 노드를 우선하여 방문하는 방식의 알고리즘입니다. 여기서 말하는 거리는 시작 노드와 목표 노드까지의 차수입니다.
다음 방식대로 진행합니다.
큐가 비었는지 확인합니다. 큐가 비어있다면 탐색이 마무리가 됐음을 나타냅니다.
큐에서 노드를 팝합니다.
팝한 노드와 인접한 모든 노드를 확인하고 그 중 아직 방문하지 않은 노드를 큐에 푸시합니다.
깊이 우선 탐색과 너비 우선 탐색 비교
깊이 우선 탐색은 깊게 탐색 후 되돌아오는 특성이 있고, 너비 우선 탐색은 시작 노드에서 인접한 노드부터 방문하는 특성을 가집니다.
깊이 탐색한 다음 되돌아오는 깊이 우선 탐색
가장 깊은 곳을 우선하여 탐색하고, 더 이상 탐색할 수 없으면 백트래킹하여 최근 방문 노드부터 다시 탐색을 진행한다는 특징이 있어서 모든 가능한 해를 찾는 백트래킹 알고리즘을 구현할 때나 그래프의 사이클을 감지해야 하는 경우 활용할 수 있습니다.
최단 경로를 찾는 문제가 아니라면 깊이 우선 탐색을 우선 고려해보는 것이 좋습니다.
최단 경로를 보장하는 너비 우선 탐색
너비 우선 탐색은 찾은 노드가 시작 노드로부터 최단 경로임을 보장합니다. 왜냐하면 가까운 간선을 통해 모든 노드를 방문하기 때문입니다.
가장 가까운 답을 찾는 문제라면 너비 우선 탐색으로 구현하면 됩니다.
그래프 최단 경로 구하기
다익스트라 알고리즘
시작 노드를 설정하고 시작 노드로부터 특정 노드까지의 최소 비용을 저장할 공간과 직전 노드를 저장할 공간을 마련합니다.
최소 비용을 저장할 공간은 모두 매우 큰 값으로 초기화 합니다. 직전 노드도 마찬가지입니다.
시작 노드의 최소 비용은 0, 직전 노드는 자신으로 합니다.
해당 노드를 통해 방문할 수 있는 노드 중, 최소 비용이 가장 적은 노드를 선택합니다.
해당 노드를 거쳐서 각 노드까지 가는 최소 비용과 현재까지 구한 최소 비용을 비교해 작은 값을 각 노드의 최소 비용으로 갱신합니다.
이때 직전 노드 값도 갱신합니다.
노드 개수에서 1을 뺀 만큼 반복합니다.
벨만-포드 알고리즘
매 단계마다 모든 간선의 가중치를 다시 확인하여 최소 비용을 갱신하므로 음의 가중치를 가지는 그래프에서도 최단 경로를 구할 수 있습니다.
시작 노드를 설정한 다음 최소 비용은 0, 나머지 노드는 무한으로 초기화 합니다. 이후 최소 비용을 갱신할 때 직전 노드도 갱신합니다.
노드 개수 -1만큼 다음 연산을 반복합니다.
시작 노드에서 갈 수 있는 각 노드에 대해 현재까지 구한 최소 비용보다 더 적은 최소 비용으로 갈 수 있는지 확인하여 갱신합니다.
2-1 과정을 마지막으로 한번 더 수행하여 갱신되는 최소 비용이 있는지 확인합니다. 있다면 음의 순환이 있음을 의미합니다.
왜 정점 개수 -1만큼 반복하는가? 매연산마다 최단 경로가 1개씩 확정되므로!
왜 한 번 더 연산을 반복하는가? 음의 순환을 찾기 위해!
음의 순환에 빠지는 건 벨만-포드 알고리즘의 한계다?
모든 알고리즘은 음의 순환이 있다면 어떤 알고리즘도 최단 경로를 구할 수 없습니다.
목적 | 장단 점 및 특징 | 시간 복잡도 | |
|---|---|---|---|
다익스트라 알고리즘 | 출발 노드로부터 도착 노드들까지의 최단 경로 찾기 | 음의 가중치를 가지는 그래프에서 최단 경로를 구할 수 없음 | |
벨만-포드 알고리즘 | 출발 노드로부터 도착 노드들까지의 최단 경로 찾기 | 음의 가중치를 가지는 그래프에서도 최단 경로를 구할 수 있고, 음의 순환도 감지할 수 있음 |